WP's HP: HOME | SloMo: Links ~ FAQ ~ Info ~ Tipps ~ Daten ~ Clips ~ HYCAM ~ Freq. ~ [f-Kalkulator] ~ Trigger ~ Bildspeicher | ?Hilfe? | English

WP's Objektiv-Kalkulator

Formatfüllende Aufnahme

Brennweitenrechner

Der einfache Kalkulator für die Distanz zum Objekt bei gegebener Brennweite und für die Brennweite bei gegebener Entfernung zum Objekt unter Voraussetzung der formatfüllenden Aufnahme. Damit erfolgt die optimale Ausnutzung der fotoaktiven Fläche des Aufnahmemediums. (JavaScript erforderlich.)
Bitte geben Sie statt des Kommas »,« einen Punkt ».« als dezimales Trennungszeichen ein. Beachten Sie auch die unterschiedlichen Maßeinheiten.

Distanz	Abbildung an dünner Linse	Brennweite
d = f × (1 + O / S)		f = d / (1 + O / S)
Brennweite f [mm]:		Distanz d [m]:
Objektgröße O [m]:		Objektgröße O [m]:
Bildgröße S [mm]:		Bildgröße S [mm]:
Berechne: m		Berechne: mm

Legende

d: Distanz zwischen Aufnahmeobjekt und Kameraobjektiv (eigentlich objektseitige Hauptebene des Abbildungssystems)
f: Brennweitenaufschrift des Objektives normalerweise in Millimeter; stimmt mit der Realität überein, wenn das Objektiv mit passendem Adapter montiert wird
O: Größte Ausdehnung des Aufnahmeobjekts senkrecht zur Aufnahmerichtung; einfacher: was man sieht. Man kann auch die Diagonale nehmen.
S: Kleinste Ausdehnung der aktiven Sensorfläche oder des Films senkrecht zur Aufnahmerichtung. Man kann auch die Diagonale nehmen. Für Werte siehe [SloMo Info].
Nebenbei: Die Sensoren sind deutlich kleiner als die Diagonalangabe des Zoll-Formats vermuten lässt. So hat ein 1 Zoll Sensor nicht etwa eine Diagonale von 25,4 mm, sondern lediglich von 15,875 mm. Dieses Verhältnis kann als »Konversionsfaktor« für andere Formate hergenommen werden.
2ω: Öffnungswinkel oder Blickfeld (engl.: angle of view) 2ω = 2 × arctan (1/2 × O / d) = 2 × arctan (1/2 × S / f'); mit der Objektivbrennweite f' (eigentlich nicht das f von der Objektivaufschrift, sondern das Auflagemaß, da Objektive üblicherweise aus einer Linsengruppe bestehen); [Werte in mm].

Tipps

Achtung: Man muss bei Standardobjektiven mindestens eines Abstand von 0,3 m (manchmal auch über 1 m) zum Objekt einhalten, sonst lassen sie sich nicht mehr scharfstellen.

Übrigens kann man die tatsächliche Sensorgröße durch Umformen obiger Gleichungen abschätzen. Objektgröße O und Objektdistanz d misst man einfach bei einer Testaufnahme, die Brennweite f ist die von der Objektivaufschrift: S = f × O / (d - f); [alle Werte in mm].

Schärfentiefe (Tiefenschärfe)

Die beiden folgenden Terme, d.h. ihre Summe, ergeben den Schärfentiefe- (auch Tiefenschärfe-) Bereich, in dem Objekte im Fokus liegen, also scharf abgebildet werden. (Alles in SI-Einheiten - Meter oder Millimeter.)
Der scharf abgebildete Bereich vor der eingestellten Entfernung ist:

d_vor = d × f² / (f² + Ø × k × (d - f))

Und der scharf abgebildete Bereich hinter dieser Entfernung ist:

d_nach = d × f² / (f² - Ø × k × (d + f))

Zeichenerklärung:

d = eingestellte Entfernung am Fokusring
f = Brennweite des Objektives
k = Blendenzahl
Ø = Durchmesser des Unschärfekreises

Der Durchmesser des Unschärfekreises ermittelt sich aus dem minimalen Abstand zweier Punkte, die das menschliche Auge aus einer gewissen Entfernung noch auflösen kann. Ein Richtwert ist 2 Winkelminuten aus 250 mm Entfernung, also ca. 0,0145 mm. Oder auch 6 Linienpaare pro Millimeter. (Streng genommen müsste man dies vom Ausgabemedium auf den Sensor bzw. Film zurückrechnen ;-) Eine Faustformel lautet: Ø = Sensor- bzw. Formatdiagonale [in mm] / 1 000 ... 1 500.

Wenn man als Abstand d die sogenannte hyperfokale Entfernung h = f × (f / (k × Ø) + 1) einstellt, erreicht man, dass der Bereich ab h/2 bis Unendlich scharf abgebildet wird. Viele einfache Kameras arbeiten so.

Bewegungsgleichungen

Damit man die Größe des interessierenden Bereiches bei bewegten Objekten und die auftretenden Geschwindigkeiten abschätzen kann, hier die Bewegungsgleichungen in einfacher Form. (Alles in SI-Einheiten Meter und Sekunden.)

Geradlinige Bewegung

Zeichenerklärung:

Geschwindigkeit: v = v(t) [m/s]; t: Zeit [s]; v₀ = v(0)
Beschleunigung: a [m/s²]; zurückgelegter Weg: w [m]

v = v₀ + a × t

w = v₀ × t + a/2 × t²

2 × a × w = v² - v₀²

Kreisbewegung

Zeichenerklärung:

Winkelgeschwindigkeit: ω = 2 × π × f; Frequenz: f = K / t = 1/T [1/s]; K: Zahl der Umläufe; t: Zeit; T: Umlaufdauer; π = 3,14
Bahnradius: r [m]

Bahngeschwindigkeit: v = r × ω

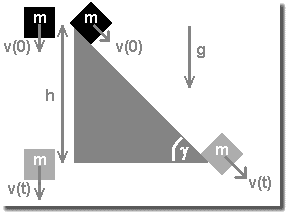
Freier Fall und Schiefe Ebene

Grundlage ist der Energieerhaltungssatz: E_pot = E_kin. Dabei kürzt sich die Masse des Objekts. Die Reibung sei vernachlässigbar. Und - wichtig - das Objekt darf keine nennenswerte Rotationsenergie aufbauen, sollte also am besten die Schräge reibungsarm hinunter gleiten. (Aber für ein Auto - Modell oder echt - tut es die Formel.)

Zeichenerklärung:

Potenzielle Energie (Lageenergie): E_pot = m × g × h; m: Masse des Objekts; Erdbeschleunigung: g = 9,81 m/s²; h: Fallhöhe bzw. Höhe der Schiefen Ebene
Kinetische Energie (Bewegungsenergie): E_kin = m/2 × v²; m: Masse des Objekts; v: Momentangeschwindigkeit des Objekts beim Aufschlag, d.h. beim Fallen um die Höhe h, bzw. beim Verlassen der Schiefen Ebene

v = √(2 × g × h)
h = 1/2 × v² / g

Spezialfälle

Denn grau ist alle Theorie...

Bewegungsunschärfe

Während der Belichtungszeit bewegt sich ein Objekt um

Δw = v × t_shutter

dem Produkt aus seiner Geschwindigkeit und der Belichtungszeit eines Bildes.

Beispiel: Ein Auto fahre mit der konstanten Geschwindigkeit v = 64 km/h = 17,78 m/s. Bei einer Aufnahmefrequenz von F = 1/ 000 Bilder/sek bewegt sich das Auto folglich um bis zu

Δw = v × t = v / F = 17,78 m/s / 1 000 Bilder/sek = 0,01778 m = 17,78 mm

während einer Aufnahme, falls man die Belichtungszeit pro Bild nicht mit einem Verschluss (engl.: shutter) verringert. Falls die Abbildung von Δw kleiner ist als ein Pixel, wird der Effekt nicht wahrgenommen.

w = 2 × d × tan ω
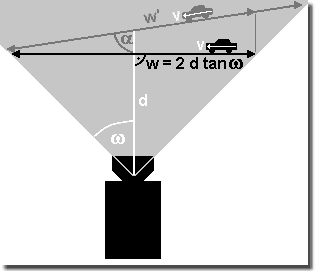
Wegverlängerung durch Schrägfahrt

Schrägfahrt - Schräger Blick auf das Objekt

Blickt die Kamera nicht rechtwinklig auf das Objekt, sondern liegt ein von 90° abweichender Winkel zwischen Kamerablickrichtung und Objekt bzw. seiner Bewegungsrichtung, fährt z.B. ein Auto auf die Kamera zu, so verringert sich die abzubildende Strecke ungefähr auf

w_{|_} = w' × sin α

mit w_{|_} als senkrechter Projektion der Fahrstrecke w' und dem Zwischenwinkel α zwischen Blickrichtung und Fahrtrichtung w'.

Wie man im Bild rechts sieht, kann man bei geeigneter Wahl sogar noch etwas Strecke hinzugewinnen.
Somit eröffnet sich die Möglichkeit räumlich bzw. zeitlich mehr aufzunehmen, das Objekt und seine Bewegung somit höher aufgelöst abzubilden.

Bei dieser Anordnung muss man allerdings die Schärfentiefe beachten, da sich der Abstand zur Kamera deutlich ändern kann.